10-CG-Rasterization

---

Overview of Rasterization

Framebuffer Model

• Raster Display: 2D array of picture elements (pixels)
• Pixels individually set/cleared (greyscale, color)
• Window coordinates: pixels centered at integers

2D Scan Conversion

Geometric primitives

• (point, line, polygon, circle, polyhedron, sphere... )

Primitives are continuous; screen is discrete

Scan Conversion:

• algorithms for efficient generation of the samples comprising this approximation

将连续的几何图元（如点、直线、多边形、圆等）转换为离散像素集合的过程，称为扫描转换（Scan Conversion）。其核心是通过算法高效地确定图元覆盖的像素，并设置相应的颜色值。

核心问题：

• 几何图元是数学上的连续对象（如直线是无限个点的集合），而屏幕是离散的像素阵列，需用有限像素近似表示图元。
• 目标：找到最接近图元的像素集合，同时保证效率（如减少浮点运算、避免冗余判断）。

典型图元的扫描转换：

1. 点（Point）：

   • 直接将坐标 $(x,y)$ 对应的像素设置为指定颜色。
   • 若坐标为非整数，需通过插值（如四舍五入）确定像素中心。

2. 直线（Line）：

   • 问题：给定两点 $(x_1,y_1)$ 和 $(x_2,y_2)$，确定覆盖的像素。
   • 算法：
     • Bresenham算法：仅用整数运算，通过误差累积确定下一个像素，效率极高。
     • 中点画线法：利用中点误差判断像素位置，适用于硬件实现。
   • 示例： 绘制从 $(1,1)$ 到 $(4,3)$ 的直线，覆盖像素为 $(1,1)$、$(2,2)$、$(3,2)$、$(4,3)$。

3. 多边形（Polygon）：

   • 问题：填充多边形内部区域对应的像素。
   • 算法：
     • 扫描线算法：按行（扫描线）遍历多边形，确定每行的像素区间，填充区间内的像素。
     • **奇偶规则（Odd-Even Rule）或非零环绕数规则（Non-Zero Winding Number Rule）**判断点是否在多边形内部。
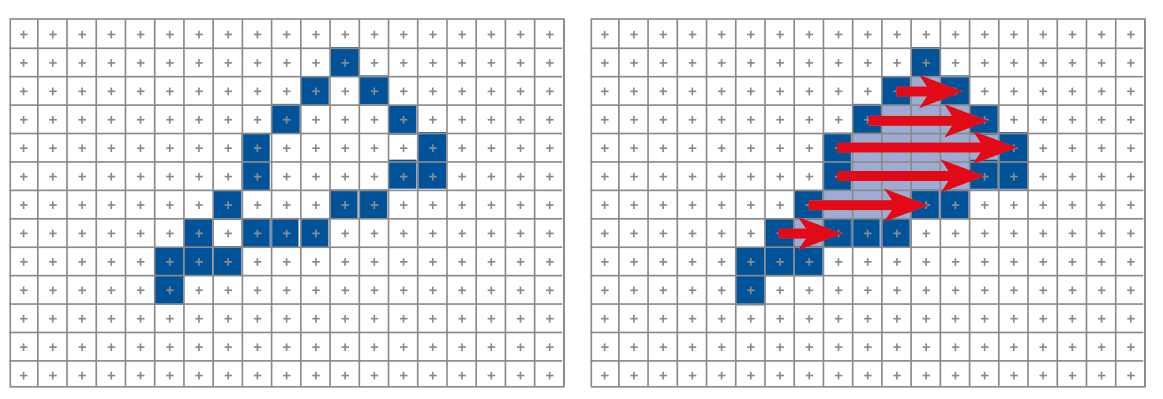
   • 示例： 左图为连续多边形，右图为扫描转换后的像素填充结果（绿色和蓝色像素）。

4. 圆（Circle）：

   • 算法：中点画圆法、Bresenham画圆法，利用对称性减少计算量（仅计算1/8圆，镜像生成其余部分）。

Brute force solution for triangles

For each pixel

• Compute line equations at pixel center
• "clip" against the triangle

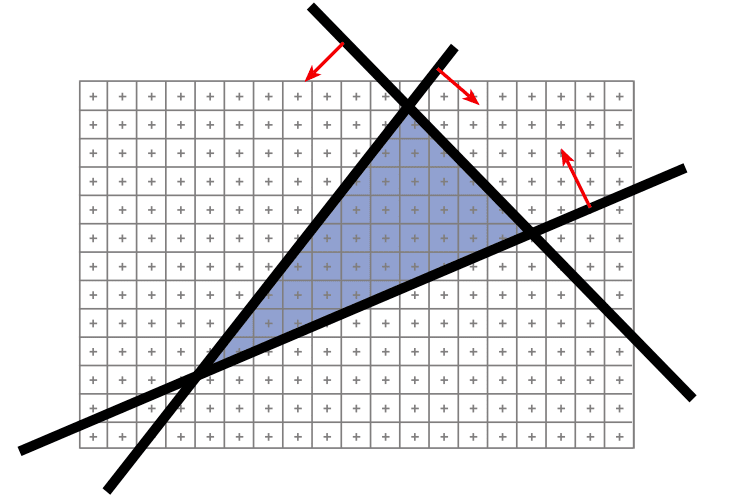
Improvement:

• Compute only for the screen bounding box of the triangle
• Xmin, Xmax, Ymin, Ymax of the triangle vertices

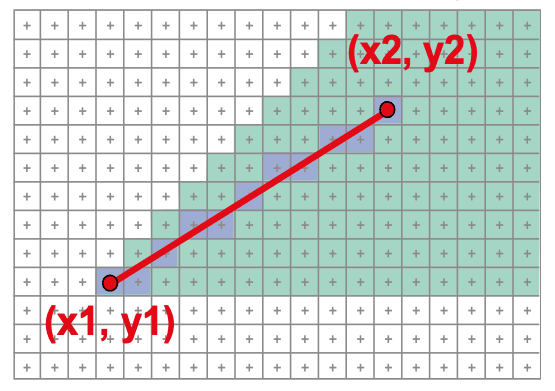
Better Solution: Line rasterization

Line Rasterization Requirements

• Transform continuous primitive into discrete samples
• Uniform thickness & brightness
• Continuous appearance
• No gaps
• Accuracy
• Speed

Algorithm Design Choices

Assume $m=\frac{dy}{dx},0<m<1$

Exactly one pixel per column

• Avoid $fewer\to disconnected$, $more\to toothick$

---

亮度变化、最大差异与抗锯齿补偿

亮度随斜率变化的原因：像素密度差异

现象描述： 当直线斜率不同时，光栅化后的像素密度不同，导致视觉亮度差异。

• 水平线段（$m=0$）：像素沿x轴密集排列，单位长度内像素数最多，亮度最高；
• 对角线段（$m=1$）：像素沿x、y轴交替排列，单位长度内像素数最少，亮度最低。

数学分析：

• 假设线段长度为 $L$，水平线段的像素数约为 $L$（dx = L），对角线段的像素数约为 $\frac{L}{\sqrt{2}}$（dx = dy = L / $\sqrt{2}$）。

• 亮度与像素数成正比，因此对角线段的亮度约为水平线段的 $1/\sqrt{2}$，即亮度差异最大可达 $\sqrt{2}$ 倍（水平线段亮度是对角线段的 $\sqrt{2}$ 倍）。

• Compensate for this

  • 抗锯齿技术: 通过调整像素亮度权重，补偿因像素离散化导致的亮度不均和锯齿，使不同斜率的线段视觉效果更一致。

---

Line Rasterization

Naive Line Rasterization Algorithm

• Simply compute $y$ as a function of $x$
  • Conceptually: move vertical scan line from $x_1$ to $x_2$
  • Set pixel $(x,round(y(x)))$

$$y=y_1+\frac{x-x_1}{x_2-x_1}(y_2-y_1)$$$$=y_1+m(x-x_1)$$$$m=\frac{dy}{dx}$$

Code

void Line (int x,, int yi, int x2, int y){
	int x;
	float dy, dx, y, m;
	dy = y2 - y1;
	dx = x2 - X1;
	m = dy/dx;
	y= y1;
	for (x = x1; x<=x2, X++) {
		WritePixel (x, round (y)) ;
		y += m;
	}
}

Efficiency

• Computing $y$ value is expensive
• Observe: $y+=m$ at each $x$ step $(m=\frac{dy}{dx})$

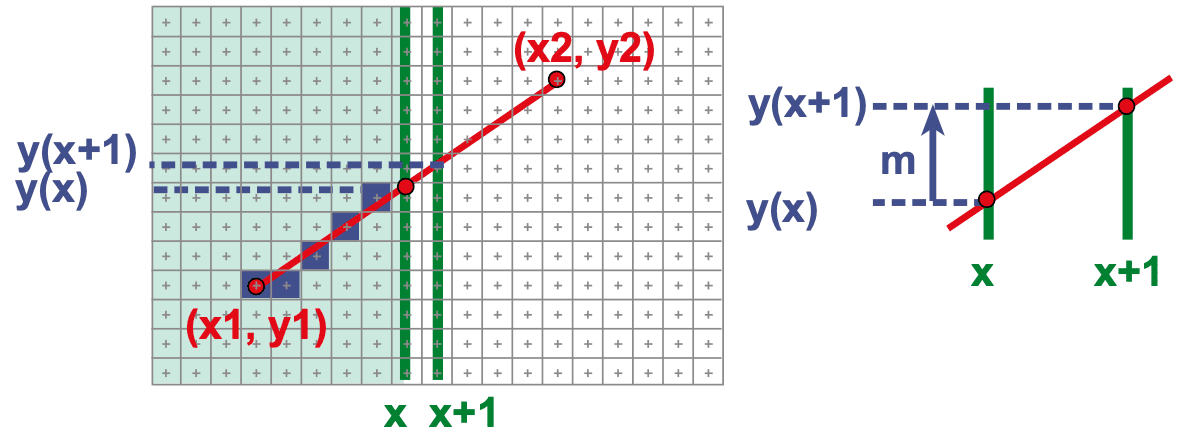
Grid Marching vs. Line Rasterization

网格行进 vs. 直线光栅化：目标驱动的方法差异** 图示对比解析：

1. 左图：光线加速（Ray Acceleration）

   • 场景：光线穿过网格，需检测所有与之相交的单元格（如红色网格）。
   • 目的：在光线追踪中加速交点计算，减少不必要的物体检测。
   • 特点：遍历所有穿过的单元格，计算量大，但确保无遗漏。

2. 中图与右图：直线光栅化

   • 场景：在像素网格中找到最接近直线的像素（如红色像素）。
   • 目的：用离散像素近似连续直线，需平衡精度与效率。
   • 特点：
     • 中图（灰色像素）：可能包含边缘模糊的抗锯齿处理；
     • 右图：纯二值化像素，严格选择最近点。

关键区别：

维度	网格行进（光线追踪）	直线光栅化
核心任务	几何相交检测	离散化采样（像素选择）
输出粒度	网格单元格（可能多个）	像素点（单个或加权像素）
计算重点	射线方向与网格交点	像素与直线的距离或误差
算法目标	无遗漏地检测所有可能相交的物体	用最少计算量生成视觉连贯的线段

• Ray Acceleration: Must examine every cell the line touches
• Line Rasterization: Best discrete approximation of the line

Bresenham's Algorithm (DDA)

• Digital differential analyzer(DDA)

Select pixel vertically closest to line segment

• intuitive, efficient,
• pixel center always within 0.5 vertically

Observation:

• If we're at pixel $P(X_p,Y_p)$, the next pixel must be either 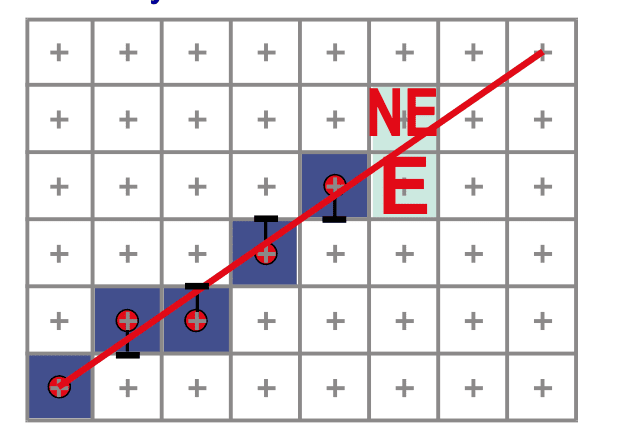$E(x_p+1,y_p)$ or $NE(x_{p+1},y_{p+1})$
• 

Which pixel to choose: E or NE?

• Choose E if segment passes below or through middle point M
• Choose NE if segment passes above M
• 

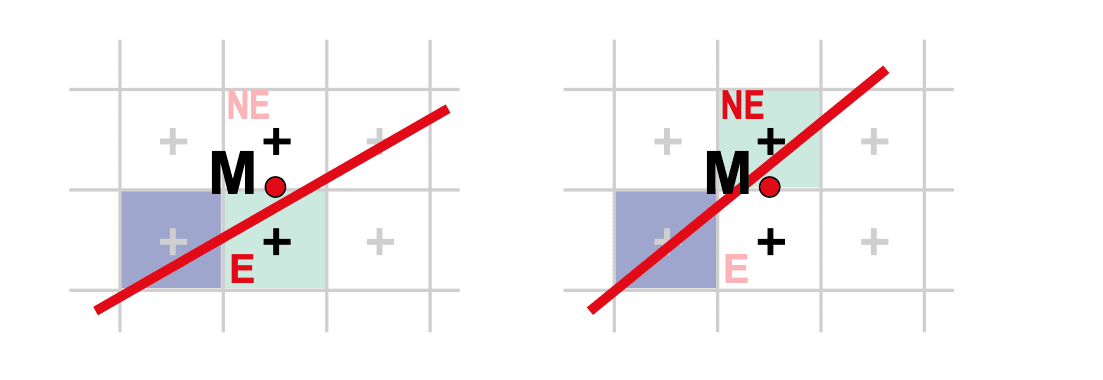
Use decision function F to identify points underlying line L:

$$F(x,y)=D=ax+by+c$$

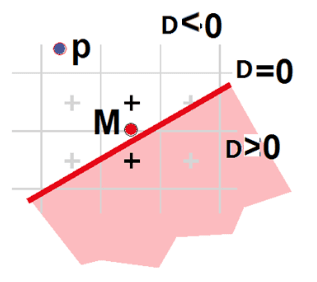
• positive below L
• zero on L
• negative above L

$M:(x_i+1,y_i+\frac{1}{2})$

• If $F(x_i+1,y_i+\frac{1}{2})<0$, M lies above the line, chose E
• If $F(X_i+1,y_i+\frac{1}{2})>0$, M lies below the line, chose NE

---

$$y=\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}x+B$$$$F(x,y)=\mathrm{\Delta }y\cdot x-\mathrm{\Delta }x\cdot y+\mathrm{\Delta }xB=0$$

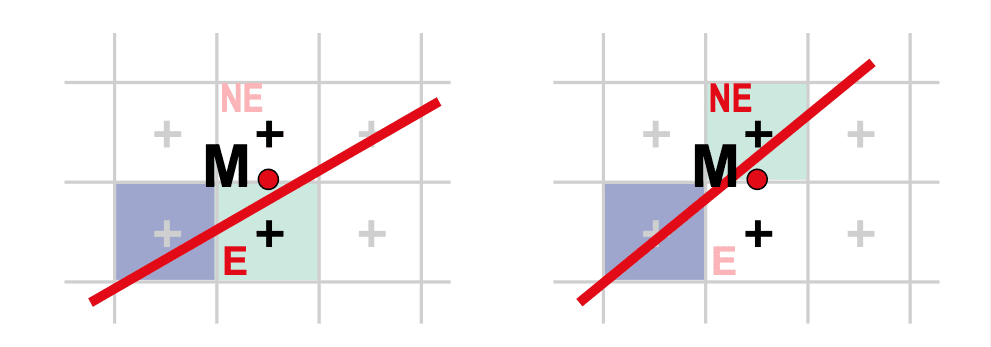
中点M的坐标： E和NE像素的中点为 $M(x_i+1,y_i+0.5)$，将其代入一般式方程 $F(x,y)$ 可得：

$$F(M)=\mathrm{\Delta }y(x_i+1)-\mathrm{\Delta }x(y_i+\frac{1}{2})+\mathrm{\Delta }xB.$$

关键问题：

• $F(M)$ 包含浮点数 $0.5$，需整数化处理以避免浮点运算。
• 决策仅需 $F(M)$ 的符号（正/负），因此可将其乘以2（符号不变）：$$d_i=2F(M)=2\mathrm{\Delta }y(x_i+1)-\mathrm{\Delta }x(2y_i+1)+2\mathrm{\Delta }xB.$$此时 $d_i$ 为整数，且：
  • $d_i<0$ → $M$ 在直线上方 → 选 $E$；
  • $d_i>0$ → $M$ 在直线下方 → 选 $NE$；
  • $d_i=0$ → 直线经过 $M$，约定选 $NE$。

决策函数的递推优化：增量计算避免重复运算目标：避免每次计算 $d_i$ 时重复代入直线方程，利用递推关系快速更新 $d_i$。

推导过程：

1. 展开 $d_i$：

   $$d_i=2\mathrm{\Delta }y{x}_i+2\mathrm{\Delta }y-2\mathrm{\Delta }x{y}_i-\mathrm{\Delta }x+2\mathrm{\Delta }xB.$$

   注意到 $F(x_i,y_i)=\mathrm{\Delta }y{x}_i-\mathrm{\Delta }x{y}_i+\mathrm{\Delta }xB=0$（因 $(x_i,y_i)$ 在直线上），故：

   $$\mathrm{\Delta }y{x}_i-\mathrm{\Delta }x{y}_i=-\mathrm{\Delta }xB\Rightarrow 2(\mathrm{\Delta }y{x}_i-\mathrm{\Delta }x{y}_i)=-2\mathrm{\Delta }xB.$$

   代入 $d_i$ 得：

   $$d_i=2F(x_i,y_i)+2\mathrm{\Delta }y-\mathrm{\Delta }x=2\mathrm{\Delta }y-\mathrm{\Delta }x(\text{因 }F(x_i,y_i)=0).$$

2. 递推关系：

   • 若选 $E$（$y$ 不变）： 下一个中点为 $(x_i+2,y_i+0.5)$，代入 $d_i$ 得：$$d_{i+1}=2\mathrm{\Delta }y(x_i+2)-\mathrm{\Delta }x(2y_i+1)+2\mathrm{\Delta }xB=d_i+2\mathrm{\Delta }y.$$
   • 若选 $NE$（$y$ 递增1）： 下一个中点为 $(x_i+2,y_i+1.5)$，代入 $d_i$ 得：$$d_{i+1}=2\mathrm{\Delta }y(x_i+2)-\mathrm{\Delta }x(2y_i+3)+2\mathrm{\Delta }xB=d_i+2\mathrm{\Delta }y-2\mathrm{\Delta }x.$$

起点 $(x_0,y_0)$： 因起点在直线上，$F(x_0,y_0)=0$，代入 $d_i$ 的初始表达式：

$$d_0=2\mathrm{\Delta }y-\mathrm{\Delta }x.$$

这是递推计算的起点，无需额外计算。

$$x_{i+1}=x_i+1$$$$y_{i+1}=\{\begin{array}{ll}{y}_i& \text{if E}\\ y_i+1& \text{if NE}\end{array}$$$$\mathrm{\Delta }d=d_{i+1}-d_i=2\mathrm{\Delta }y(x_{i+1}-x_i)-2\mathrm{\Delta }x(y_{i+1}-y_i)$$$$\mathrm{\Delta }d=\{\begin{array}{ll}2\mathrm{\Delta }y& \text{if E (incr E)}\\ 2\mathrm{\Delta }y-2\mathrm{\Delta }x& \text{if NE (incr NE)}\end{array}$$

void BresenhamLine(int x0, int y0, int xn, int yn) {
    int dx, dy, incrE, incrNE, d, x, y;
    dx = xn - x0;       // x方向总增量（假设xn > x0）
    dy = yn - y0;       // y方向总增量（正斜率时dy > 0）
    d = 2*dy - dx;      // 初始决策变量d0 = 2Δy - Δx
    incrE = 2*dy;       // 选择E像素时d的增量（2Δy）
    incrNE = 2*dy - 2*dx; // 选择NE像素时d的增量（2Δy - 2Δx）
    x = x0; y = y0;     // 初始化当前像素为起点
    DrawPixel(x, y);    // 绘制起点
    while (x < xn) {    // 逐列扫描，x从起点到终点
        if (d <= 0) {   // 若d≤0，直线在中点M下方或经过M，选E像素
            d += incrE; // d更新为d + 2Δy
            x++;        // 右移一列（y不变）
        } else {        // 若d>0，直线在中点M上方，选NE像素
            d += incrNE; // d更新为d + 2Δy - 2Δx
            x++; y++;   // 右移一列且上移一行
        }
        DrawPixel(x, y); // 绘制当前像素
    }
}

Example

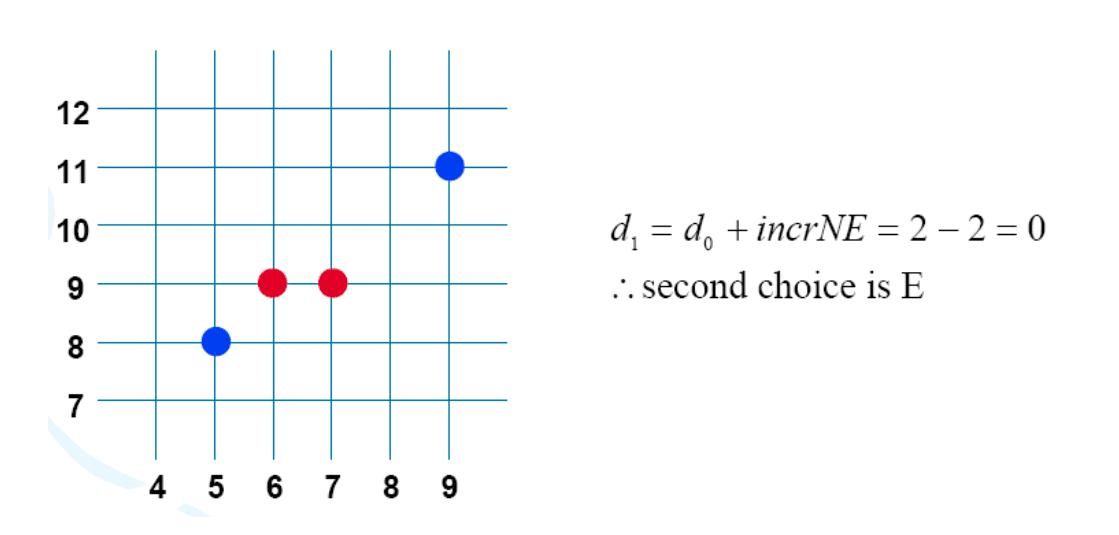
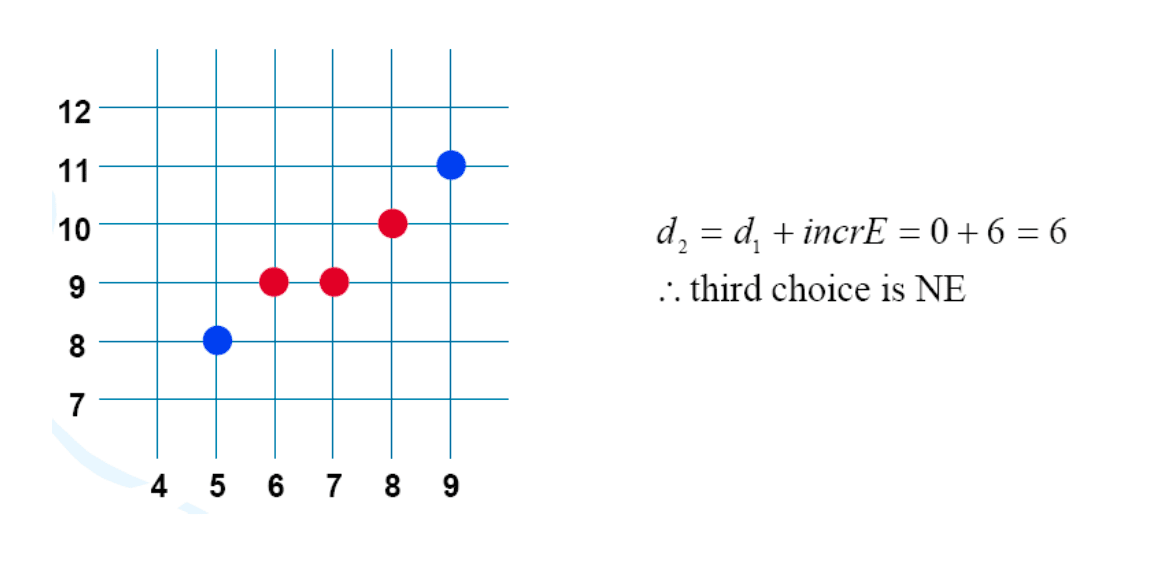
Filling Polygons

Scan Line Algorithm

• Compute the bounding pixels
• Fill the span

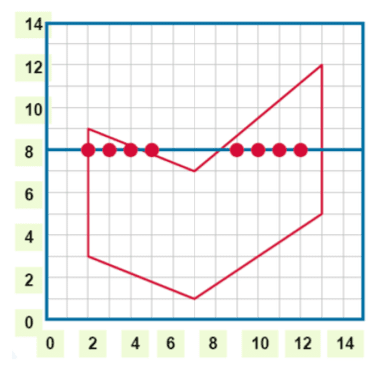
1. Find the intersections of current scan line with all edges of the polygon.
2. Sort the intersections by increasing x coordinate.
3. Fill in pixels that lie between pairs of intersections that lie interior to the polygon using the odd/even parity rule.

• Parity: even, change parity once encounter an edge
• Special parity: no change of the parity (draw 1 pixel)

Construction Edge Table

Circle Rasterization

Generate pixels for 2nd octant only

slope progress from $0\to -1$

Analog of Bresenham Segment Algorithm

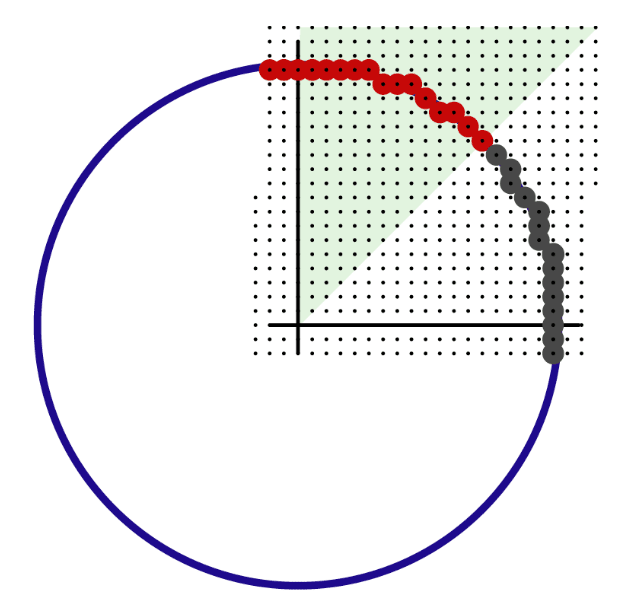
Decision Function

$$D(x,y)=x^2+y^2-R^2$$

• $D(x,y)<0$, point in the circle
• $D(x,y)=0$, point on the circle
• $D(x,y)>0$, point not in the circle

Initialize:

error term $e=-D(x,y)$

On each iteration: update x: $x^{\prime }=x+1$ update e: $e^{\prime }=e+2x+1$ if ($e\ge 0.5$): $y^{\prime }=y$ (Choose pixel E) if ($e<0.5$): $y^{\prime }=y-1$ (Choose pixel SE), $e^{\prime }=e+1$

误差项设计

为避免浮点运算，引入误差项 $e=-D(x,y)=R^2-x^2-y^2$，其含义为：

• $e>0$：点在圆内（因 $D<0$）；
• $e=0$：点在圆上；
• $e<0$：点在圆外（因 $D>0$）。

目标：通过比较 $e$ 与 $0.5$（像素中心距离的阈值），决定下一个像素是选右侧（E）还是右下（SE）。

算法步进逻辑：从$(0,R)$到$(\frac{R}{\sqrt{2}},\frac{R}{\sqrt{2}})$

初始点：圆心为 $(0,0)$ 时，第二八分圆的起点为 $(0,R)$，初始误差项：

$$e_0=R^2-0^2-R^2=0.$$

每步操作：

1. x递增1：$x\leftarrow x+1$（因在第二八分圆，x方向单增）。
2. 更新误差项：$$e^{\prime }=e-(2x+1).\text{（因 }{x}^2\text{ 增量为 }2x+1\text{）}$$
3. 判断是否需要调整y：
   • 若 $e^{\prime }\ge 0.5$：点仍在圆内，y不变，选右侧像素E $(x+1,y)$；
   • 若 $e^{\prime }<0.5$：点接近圆外，y递减1，选右下像素SE $(x+1,y-1)$，并修正误差项：$$e' = e' + (2y - 1).$$ 因 $y^2$ 增量为 $-2y+1$，即误差项增量为$-(-2y+1)=2y-1$

void CircleRasterization(int xc, int yc, int R) {
    int x = 0, y = R;
    float e = 0; // 误差项初始化为0
    DrawOctants(xc, yc, x, y); // 绘制八对称像素

    while (x < y) {
        x++;
        e -= 2 * x + 1; // 更新误差项（x递增1）
        if (e < 0.5) { // 需调整y
            y--;
            e += 2 * y - 1; // y递减1，更新误差项
        }
        DrawOctants(xc, yc, x, y); // 绘制当前像素的八对称点
    }
}

void DrawOctants(int xc, int yc, int x, int y) {
    // 绘制八对称的8个像素
    SetPixel(xc + x, yc + y);
    SetPixel(xc + y, yc + x);
    SetPixel(xc + y, yc - x);
    SetPixel(xc + x, yc - y);
    SetPixel(xc - x, yc - y);
    SetPixel(xc - y, yc - x);
    SetPixel(xc - y, yc + x);
    SetPixel(xc - x, yc + y);
}